Birthday Paradox

A paradox is a statement that contradicts itself, and yet might be true (or wrong) at the same time. So here we are, talking about the birthday paradox. If you want to understand this paradox better, we suggest you read up on your probability notes first.

Or is it happy birthday to a million people out there?

Imagine being told this - "Believe it or not, in a room with 23 people, there's a 50-50 chance of two people having the same birthday. In a room with 75 people, the chance of two people having the same birthday becomes 99.999%." 

Believe it or not?

Let's break down the problem here...

The first person can have any birthday. That gives him a 365 out of 365 possible birthdays, so the probability of the first person having the "right" birthday is 365/365 = 1.

Now, let's bring the second person into the picture. The chance of him having the same birthday as the first person is 1 out of 365. To find the probability of these two people having the same birthday, we multiply their separate probability = (365/365) * (1/365) = 1/365.

What about three people? The probability of the first and second person sharing the same birthday is still 1/365. The probability of the first and third person sharing the same birthday is 1/365 as well. What if the second and third person have the same birthday or all three people have the same birthday? Things are getting way too confusing now...

To solve this, we need to use a basic rule of probability which is the sum of the probability of the event occurring and probability of the event not occurring = 1. With this, let's start over again...

The probability of the second person not having the same birthday as the first is 364/365.

The probability of both the second and third person not having the same birthday is (365/365) * (364/365) * (363/365) = 0.9918.

The probability of four people having different birthdays will then be (365/365) * (364/365) * (363/365) * (362/365) = 0.9836.

If we keep calculating, we will see the number closing towards 0.5 as we reach 23 people, which means that there is a 50-50 chance of 2 out of 23 people having the same birthday. As we reach 75 people, the probability of 75 people having different birthdays will be close to 0 which means a 99.9% chance of 2 out of 75 people having the same birthday!

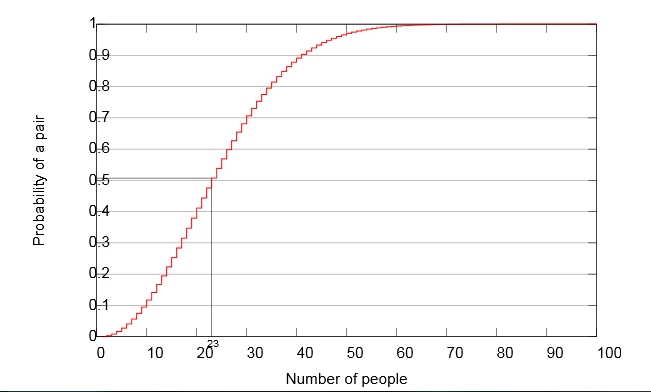This graph gives you a rough idea of how the probability of two people having the same birthday increases exponentially as the number of people increase

So why is this a paradox? 

Let's read this article and understand it better. At the end of it, do try out the interactive example to convince yourself fully. Have fun!

Conclusion

The birthday paradox is actually a tautology i.e. true all the time. It is a paradox only because we are selfish humans (refer to article above).  The next time you have difficulty starting a conversation, why not share with someone about this paradox, it is a rather interesting topic to share about isn't it?